What is correlation?
A correlation coefficient measures the extent to which two variables tend to change together. The coefficient describes both the strength and the direction of the relationship. Minitab offers two different correlation analyses:
Pearson product moment correlation
The Pearson correlation evaluates the linear relationship between two continuous variables. A relationship is linear when a change in one variable is associated with a proportional change in the other variable.
For example, you might use a Pearson correlation to evaluate whether increases in temperature at your production facility are associated with decreasing thickness of your chocolate coating.
Spearman rank-order correlation
The Spearman correlation evaluates the monotonic relationship between two continuous or ordinal variables. In a monotonic relationship, the variables tend to change together, but not necessarily at a constant rate. The Spearman correlation coefficient is based on the ranked values for each variable rather than the raw data.
Spearman correlation is often used to evaluate relationships involving ordinal variables. For example, you might use a Spearman correlation to evaluate whether the order in which employees complete a test exercise is related to the number of months they have been employed.
It is always a good idea to examine the relationship between variables with a scatterplot. Correlation coefficients only measure linear (Pearson) or monotonic (Spearman) relationships. Other relationships are possible.
Comparison of Pearson and Spearman coefficients
The Pearson and Spearman correlation coefficients can range in value from −1 to +1. For the Pearson correlation coefficient to be +1, when one variable increases then the other variable increases by a consistent amount. This relationship forms a perfect line. The Spearman correlation coefficient is also +1 in this case.

If the relationship is that one variable increases when the other increases, but the amount is not consistent, the Pearson correlation coefficient is positive but less than +1. The Spearman coefficient still equals +1 in this case.

When a relationship is random or non-existent, then both correlation coefficients are nearly zero.

If the relationship is a perfect line for a decreasing relationship, then both correlation coefficients are −1.

If the relationship is that one variable decreases when the other increases, but the amount is not consistent, then the Pearson correlation coefficient is negative but greater than −1. The Spearman coefficient still equals −1 in this case

Correlation values of −1 or 1 imply an exact linear relationship, like that between a circle's radius and circumference. However, the real value of correlation values is in quantifying less than perfect relationships. Finding that two variables are correlated often informs a regression analysis which tries to describe this type of relationship more.
Other nonlinear relationships
Pearson correlation coefficients measure only linear relationships. Spearman correlation coefficients measure only monotonic relationships. So a meaningful relationship can exist even if the correlation coefficients are 0. Examine a scatterplot to determine the form of the relationship.
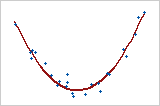
This graph shows a very strong relationship. The Pearson coefficient and Spearman coefficient are both approximately 0.
Questions:
- How do you define correlation?
- What are the commonly used analyses for correlation?
- Draw an illustration / graph where both Pearson and Spearman = -1
Note: the passage is a repost from Minitab's official website